Activity 1:

Computing the Even Numbers in Two Ways

CHALLENGE

Can the same thing be made using all the numbers once and also using every other number once?

Task A: Doubling each term in a sequence

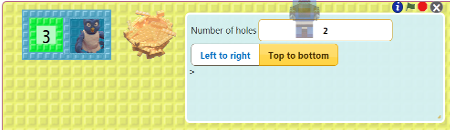
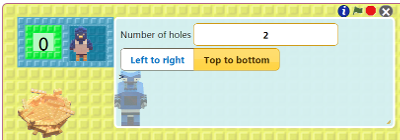
Train a robot called Doubler that receives a number on a nest and gives a bird twice that number. See the illustrated instructions for training this robot. Test out your Doubler robot by dragging a copy of him to the back of the box below and then clicking either green flag:


{ "semantic": { "type": "top_level", "backside_widgets": [ { "widget": { "semantic": { "type": "bird", "nest": { "shared_widget_index": 0 } }, "view": { "frontside_width": 70, "frontside_height": 102, "frontside_left": 33, "frontside_top": 27.8125 }, "version": 1 } }, { "widget": { "semantic": { "type": "element", "html": "Input", "attributes": [], "attribute_values": [] }, "view": { "frontside_left": 46, "frontside_top": 145.8125 }, "version": 1 } }, { "widget": { "shared_widget_index": 2 }, "is_backside": true }, { "widget": { "semantic": { "type": "number", "operator": "+", "numerator": "1", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 23, "frontside_top": 272 }, "version": 1 } }, { "widget": { "semantic": { "type": "number", "operator": "+", "numerator": "2", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 128, "frontside_top": 275, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } }, { "widget": { "semantic": { "type": "number", "operator": "+", "numerator": "3", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 235, "frontside_top": 277, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } }, { "widget": { "semantic": { "type": "number", "operator": "+", "numerator": "4", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 343, "frontside_top": 279, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } }, { "widget": { "semantic": { "type": "number", "operator": "+", "numerator": "5", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 448, "frontside_top": 278, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } }, { "widget": { "shared_widget_index": 1 } }, { "widget": { "semantic": { "type": "element", "html": "Output", "attributes": [], "attribute_values": [] }, "view": { "frontside_left": 157, "frontside_top": 144.8125 }, "version": 1 } }, { "widget": { "shared_widget_index": 2 } } ] }, "view": { "background_color": "rgba(245, 240, 240, 0.941176)", "frontside_width": 0, "frontside_height": 0, "backside_width": 870, "backside_height": 347, "backside_left": 8, "backside_top": 185.1875, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 886, "original_height": 347 }, "drag_x_offset": 697, "drag_y_offset": 326.8125, "backside": true }, "version": 1, "shared_widgets": [ { "semantic": { "type": "nest", "contents": [], "guid": "toontalk_id_1413118519635", "waiting_robots": [] }, "view": { "backside_geometry": { "x_scale": 0.5567375886524821, "y_scale": 1, "original_width": 564, "original_height": 200 }, "saved_width": 116, "saved_height": 141 }, "version": 1 }, { "semantic": { "type": "nest", "contents": [], "guid": "toontalk_id_1413285158417", "waiting_robots": [] }, "view": { "frontside_width": 116, "frontside_height": 98, "frontside_left": 132, "frontside_top": 38 }, "version": 1 }, { "semantic": { "type": "box", "size": 2, "contents": [ { "shared_widget_index": 0 }, { "semantic": { "type": "bird", "nest": { "shared_widget_index": 1 } }, "view": { "saved_width": 103, "saved_height": 117 }, "version": 1 } ], "horizontal": true, "backside_widgets": [ { "widget": { "semantic": { "type": "element", "html": "drop%20your%20robot%20here", "attributes": [ "width" ], "attribute_values": [ "240" ] }, "view": { "frontside_left": 124.56182861328125, "frontside_top": 200.23202514648438, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } } ] }, "view": { "frontside_width": 164, "frontside_height": 68, "frontside_left": 281, "frontside_top": 41, "backside_width": 550, "backside_height": 253, "backside_left": 513, "backside_top": 32, "backside_geometry": { "x_scale": 0.6094776859504129, "y_scale": 3.95455189254707, "original_width": 171, "original_height": 39 } }, "version": 1 } ] }

Give the input bird 1, and then 2, 3, 4, and 5. What numbers appear on the output nest?

If Doubler is working as it should then whatever number you give the input bird you should get twice that number on the output nest.

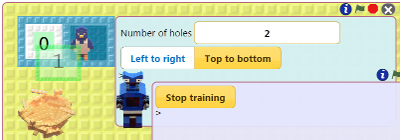
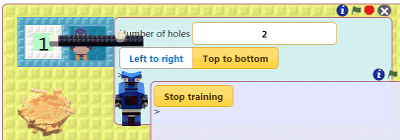
Let's give Doubler all the natural numbers (1, 2, 3, and so on forever). Since we can't type in all the natural numbers we'll need a robot to help us. We'll call him Add 1 since that is what he'll do over and over again. Visit the instructions for how to build Add 1.

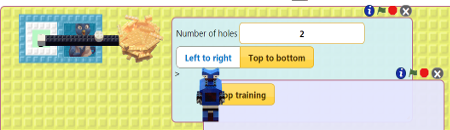
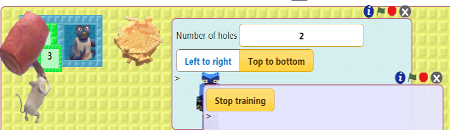
To test the Add 1 robot out go back to where you trained the robot and click the green flag. Watch what numbers end up on the nest. Stop it by clicking the stop sign. Try closing the backside of the box and run it again.

Try connecting Doubler to the sequence of natural numbers made by the Add 1 robot. You can do this by dragging the nest of Add 1 to the empty hole of the box with the Doubler robot on the back. Click the green flag of both the Add 1 and Doubler work areas and watch. You should see the bird from Add 1 bringing numbers to Doubler whose bird delivers those numbers doubled. Click the stop signs to stop things.

Did you notice that the first numbers coming out are even?

Will there ever be an odd number?


Task B: Removing every other term in a sequence

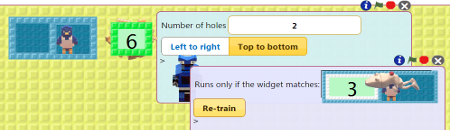
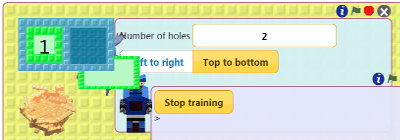
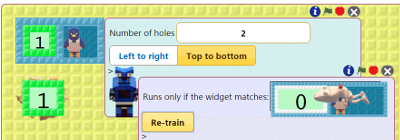
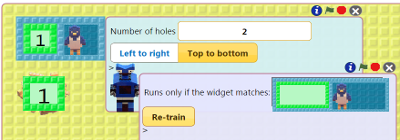
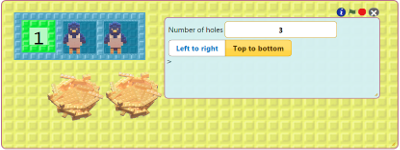
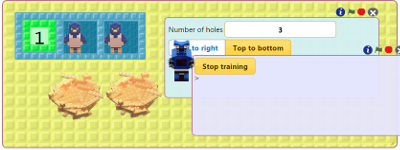
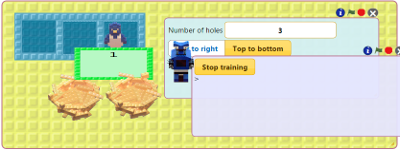
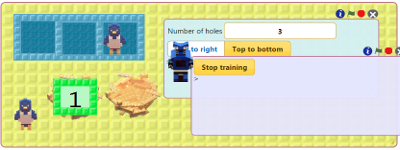
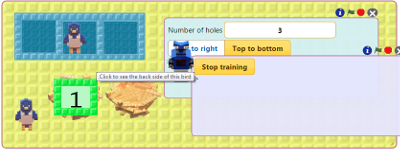
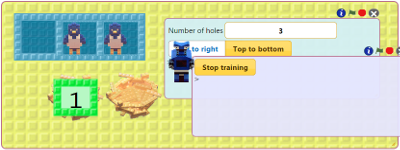
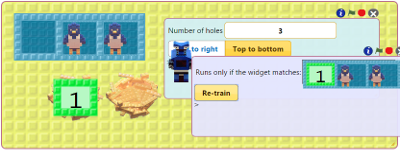
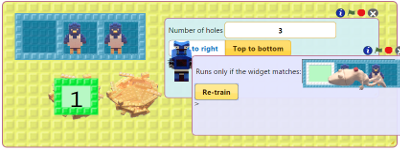
Train a robot called Split. As numbers arrive on the input nest Split gives them alternatively to two birds. The nests of the birds should receive every other number. See the instructions for training Split.

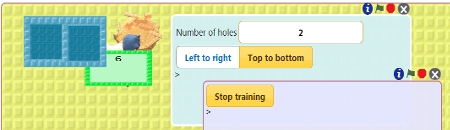
Drag the nest with the natural numbers in the first hole of Split's box. Click on the green flag.

What kind of numbers end up in the first bird's nest?

What kind of numbers end up in the second bird's nest?

Task C: Thinking about the two ways of making all the even numbers

Copy the nest that will receive all the natural numbers produced by the Add 1 robot. Start up the Add 1 robot and you should see each copy of the nest receiving 1, 2, 3 and so on.

Give one copy of the natural numbers nest to your Doubler robot and the other to the Split robot. Start all of them running and observe carefully.

If all the robots ran forever would there be a difference between the numbers that are one of Split's nests and the output nest of Doubler?

If there is a difference, what is it?

If there is no difference, how can they be the same sequence if Doubler uses every natural number and Split puts only half of the numbers on B's nest?


Task D: Even numbers dancing with natural numbers

If you saw a room full of boys and girls and everyone was dancing with a partner of the opposite sex, could you figure out if there was the same number of boys as girls? Without counting!

How would you convince someone you are right?




Imagine that you are running the Doubler robot and that after the Add 1 robots gives a bird a number it is copied and begins dancing with the output number of the Doubler robot. So 1 dances with 2, 2 with 4, 3 with 6, and so on.

If this continued forever would every even number be dancing with a natural number?

Would every natural number be dancing with an even number?

What does this tell you about how many even numbers there are?


You may be confused at this point. Infinity confused some of the world's best mathematicians. Galileo Galilei wrote in 1638 about how one line of reasoning leads you to think the sequences have the same number of numbers while another line of reasoning leads you to think there are fewer even numbers.

What do you think?

If you think they all pair up then how do you explain that the sequence of natural numbers contains all the even and all the odd numbers?

If you don't think they pair up, what is different from the room of boys and girls?


Appendix: Help with Training the Robots

Activity 1, Task A: One way to Train the Doubler Robot

Hover the mouse over a picture for more help.

{ "semantic": { "type": "number", "operator": "+", "numerator": "1", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 57, "frontside_top": 82, "drag_x_offset": 19, "drag_y_offset": 46 }, "version": 1 }
{ "semantic": { "type": "box", "size": 2, "contents": [ null, null ], "horizontal": true }, "view": { "frontside_width": 164, "frontside_height": 68, "frontside_left": 268, "frontside_top": 53, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 171, "original_height": 39 }, "drag_x_offset": 68, "drag_y_offset": 66 }, "version": 1 }
{ "semantic": { "type": "nest", "contents": [] }, "view": { "frontside_width": 116, "frontside_height": 141 }, "version": 1 }
{"semantic":{"type":"robot","body":{"type":"body","steps":[],"run_once":false}}, "view": {"drag_x_offset":31,"drag_y_offset":48}}
{ "semantic": { "type": "wand" }, "view": { "frontside_width": 191, "frontside_height": 31, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "vacuum" }, "view": { "frontside_width": 123, "frontside_height": 45, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "top_level", "backside_widgets": [ { "widget": { "semantic": { "type": "element", "html": "%3Cspan%20style%3D%22color%3A%20rgb(0%2C%200%2C%200)%3B%20font-family%3A%20Tahoma%2C%20'Trebuchet%20MS'%3B%20font-size%3A%2017.6000003814697px%3B%20font-style%3A%20normal%3B%20font-variant%3A%20normal%3B%20font-weight%3A%20normal%3B%20letter-spacing%3A%20normal%3B%20line-height%3A%20normal%3B%20orphans%3A%20auto%3B%20text-align%3A%20start%3B%20text-indent%3A%200px%3B%20text-transform%3A%20none%3B%20white-space%3A%20normal%3B%20widows%3A%20auto%3B%20word-spacing%3A%200px%3B%20-webkit-text-stroke-width%3A%200px%3B%20float%3A%20none%3B%20display%3A%20inline%20!important%3B%20z-index%3A%20108%3B%22%3ETrain%20the%20Doubler%20robot%20here%3C%2Fspan%3E", "attributes": [ "width" ], "attribute_values": [ "260" ] }, "view": { "frontside_width": 260, "frontside_height": 22, "frontside_left": 17, "frontside_top": 11.8125, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } } ] }, "view": { "background_color": "rgba(245, 240, 240, 0.941176)", "frontside_width": 0, "frontside_height": 0, "backside_width": 825, "backside_height": 416, "backside_left": 8, "backside_top": 185.1875, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 1200, "original_height": 475 }, "drag_x_offset": 181, "drag_y_offset": 165.8125, "backside": true }, "version": 1 }
Return to the task.

Activity 1, Task A: One Way to Train the Add 1 Robot

{ "semantic": { "type": "number", "operator": "+", "numerator": "1", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 57, "frontside_top": 82, "drag_x_offset": 19, "drag_y_offset": 46 }, "version": 1 }
{ "semantic": { "type": "box", "size": 2, "contents": [ null, null ], "horizontal": true }, "view": { "frontside_width": 164, "frontside_height": 68, "frontside_left": 268, "frontside_top": 53, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 171, "original_height": 39 }, "drag_x_offset": 68, "drag_y_offset": 66 }, "version": 1 }
{ "semantic": { "type": "nest", "contents": [] }, "view": { "frontside_width": 116, "frontside_height": 141 }, "version": 1 }
{"semantic":{"type":"robot","body":{"type":"body","steps":[],"run_once":false}}, "view": {"drag_x_offset":31,"drag_y_offset":48}}
{ "semantic": { "type": "wand" }, "view": { "frontside_width": 191, "frontside_height": 31, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "vacuum" }, "view": { "frontside_width": 123, "frontside_height": 45, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "top_level", "backside_widgets": [ { "widget": { "semantic": { "type": "element", "html": "%3Cspan%20style%3D%22color%3A%20rgb(0%2C%200%2C%200)%3B%20font-family%3A%20Tahoma%2C%20'Trebuchet%20MS'%3B%20font-size%3A%2017.6000003814697px%3B%20font-style%3A%20normal%3B%20font-variant%3A%20normal%3B%20font-weight%3A%20normal%3B%20letter-spacing%3A%20normal%3B%20line-height%3A%20normal%3B%20orphans%3A%20auto%3B%20text-align%3A%20start%3B%20text-indent%3A%200px%3B%20text-transform%3A%20none%3B%20white-space%3A%20normal%3B%20widows%3A%20auto%3B%20word-spacing%3A%200px%3B%20-webkit-text-stroke-width%3A%200px%3B%20float%3A%20none%3B%20display%3A%20inline%20!important%3B%20z-index%3A%20108%3B%22%3ETrain%20the%20Add%201%20robot%20here%3C%2Fspan%3E", "attributes": [ "width" ], "attribute_values": [ "260" ] }, "view": { "frontside_width": 260, "frontside_height": 22, "frontside_left": 17, "frontside_top": 11.8125, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } } ] }, "view": { "background_color": "rgba(245, 240, 240, 0.941176)", "frontside_width": 0, "frontside_height": 0, "backside_width": 825, "backside_height": 416, "backside_left": 8, "backside_top": 185.1875, "backside_geometry": { "x_scale": 1, "y_scale": 1 }, "drag_x_offset": 350, "drag_y_offset": 219.8125, "backside": true }, "version": 1 }
Return to the task.

Activity 1, Task B: One Way to Train the Split Robot


{ "semantic": { "type": "number", "operator": "+", "numerator": "1", "denominator": "1", "format": "improper_fraction" }, "view": { "frontside_width": 76, "frontside_height": 55, "frontside_left": 57, "frontside_top": 82, "drag_x_offset": 19, "drag_y_offset": 46 }, "version": 1 }
{ "semantic": { "type": "box", "size": 2, "contents": [ null, null ], "horizontal": true }, "view": { "frontside_width": 164, "frontside_height": 68, "frontside_left": 268, "frontside_top": 53, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 171, "original_height": 39 }, "drag_x_offset": 68, "drag_y_offset": 66 }, "version": 1 }
{ "semantic": { "type": "nest", "contents": [] }, "view": { "frontside_width": 116, "frontside_height": 141 }, "version": 1 }
{"semantic":{"type":"robot","body":{"type":"body","steps":[],"run_once":false}}, "view": {"drag_x_offset":31,"drag_y_offset":48}}
{ "semantic": { "type": "wand" }, "view": { "frontside_width": 191, "frontside_height": 31, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "vacuum" }, "view": { "frontside_width": 123, "frontside_height": 45, "frontside_left": 6, "frontside_top": 6 }, "version": 1 }
{ "semantic": { "type": "top_level", "backside_widgets": [ { "widget": { "semantic": { "type": "element", "html": "Train%20the%20Split%20robot%20here", "attributes": [ "width", "font-weight" ], "attribute_values": [ "260", "800" ] }, "view": { "frontside_left": 21, "frontside_top": 13.8125, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 550, "original_height": 200 } }, "version": 1 } } ] }, "view": { "background_color": "rgba(245, 240, 240, 0.941176)", "frontside_width": 0, "frontside_height": 0, "backside_width": 825, "backside_height": 416, "backside_left": 8, "backside_top": 185.1875, "backside_geometry": { "x_scale": 1, "y_scale": 1, "original_width": 1200, "original_height": 475 }, "drag_x_offset": 343, "drag_y_offset": 211.8125, "backside": true }, "version": 1 }
Return to the task.